F#による画像アーキビスト
2025-04-14 22:00:25
原文: Picture archivist in F# by Mark Seemann
F#で関数型アーキテクチャを実装する、包括的なコード例。
この記事では、以前の記事で紹介した「画像アーキビスト」アーキテクチャをF#で実装する方法を紹介します。簡単に言えば、撮影日時メタデータに基づいて画像ファイルをディレクトリに移動する、というタスクです。アーキテクチャの基本的な考え方は、ディスク上のディレクトリ構造をメモリ内のツリーとして読み込み、そのツリーを操作し、最終的にそのツリーに基づいて必要な処理を実行するというものです。
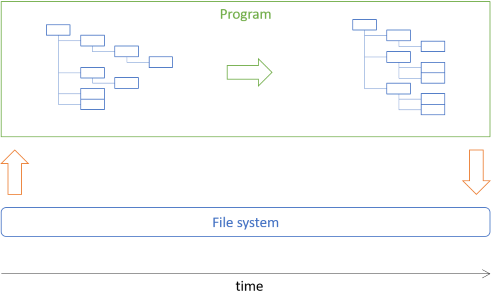
プログラムの大部分では、このツリーデータ(不変なデータ構造)を操作します。
前回の記事では、この画像アーキビストのアーキテクチャをHaskellで実装する方法を紹介しました。今回の記事では、これをF#で実装する方法を紹介します。基本的にはそのHaskellコードを移植したものです。
木構造
まずはRose木を定義することから始めましょう:
type Tree<'a, 'b> = Node of 'a * Tree<'a, 'b> list | Leaf of 'b
必要であれば、Tree関連のコードをすべて再利用可能なライブラリにまとめることもできます。というのも、このコードは特定のアプリケーション(例えば画像の移動)に依存していないからです。また、以下に紹介する関数群に対して包括的なテストスイートを書くこともできますが、この記事ではそこまで行いません。
このツリーは、内部ノードとリーフノードを明示的に区別していることに注目してください。これは、ディレクトリ名(内部ノード)を保持する必要がある一方で、リーフには追加情報(後述)を持たせたいという要件があるためです。
私は通常、F#の型定義をモジュール外に記述することが多いのですが(たとえば、Tree.Treeのようにモジュール名のプレフィックスを書く必要がなくなるため)、ツリーに関するコードの残りはすべてモジュールにまとめ、次の2つの補助関数も含めています:
module Tree =
// 'b -> Tree<'a,'b>
let leaf = Leaf
// 'a -> Tree<'a,'b> list -> Tree<'a,'b>
let node x xs = Node (x, xs)
leaf関数はそこまで重要ではありませんが、node関数はNodeケースコンストラクタのカリー化された形式を提供するので、時々便利です。
ツリーに関するその他のコードもTreeモジュール内に定義されていますが、この記事では独立した関数のように書式を整えて紹介していきます。コードの構成がわかりにくければ、GitHub上でコード全体を見ることができます。
Rose木のカタモルフィズムは、以下のcata関数です:
// ('a -> 'c list -> 'c) -> ('b -> 'c) -> Tree<'a,'b> -> 'c
let rec cata fd ff = function
| Leaf x -> ff x
| Node (x, xs) -> xs |> List.map (cata fd ff) |> fd x
Haskellでの実装ではこの関数をfoldTreeと名付けていましたが、ここではなぜ名前を変えたのでしょうか? 簡単に言えば、HaskellとF#では命名規則が異なるからです。私はHaskellから学ぶことを好みますが、それでもF#のコードはできるだけ慣用的なものにしたいのです。
呼び出し側のコードがTreeモジュール名を使って関数を参照する必要があるわけではありませんが、モジュール名付きで使っても自然な名前になるようにしたいと考えています。Tree.foldTreeと書くのは冗長に感じられますし、よりF#らしい名前はfoldなのですが、foldという名前は通常リストに偏ったfold(Haskellでいうfoldl)を意味するため、別の用途にとっておきたいのです。
というわけで、cataという名前にしました。
この記事で使われるツリーの処理は(例外を1つ除いて)すべてcataを直接または間接的に用いて実装されています。
ツリーのフィルタリング
ツリーの内容をフィルタリングできるようにしておくと便利です。たとえば、この画像アーキビストのプログラムでは、メタデータが有効な画像ファイルだけを移動する必要があります。つまり、画像ファイルでないものや、有効なメタデータを持っていない画像ファイルを除外する必要があります。
ここで便利なのが、option型(オプション型)のリーフを持つツリーから、None値を取り除く関数です。これはF#のList.chooseに似ているので、Tree.chooseと名付けました:
// ('a -> 'b option) -> Tree<'c,'a> -> Tree<'c,'b> option
let choose f = cata (fun x -> List.choose id >> node x >> Some) (f >> Option.map Leaf)
この関数の型を見て驚かれるかもしれません。なぜ戻り値が単なるTreeではなく、Tree option(ツリーのオプション)なのでしょうか?
List.chooseが単にリストを返せるのは、リストが空でもよいからです。一方で、ここで定義しているTree型には「空のツリー」という概念がありません。Tree.chooseの目的がNoneをすべて捨てることだとしたら、Leaf Noneをどう返せばよいのでしょうか?
Leafを返すには、中に入れる値が必要ですが、Noneなので値がありません。同様に、Nodeを返すにも中に入れる値がないので無理です。
このようなケースに対応するため、関数の戻り値をNoneにする必要があります:
> let l : Tree<string, int option> = Leaf None;;
val l : Tree<string,int option> = Leaf None
> Tree.choose id l;;
val it : Tree<string,int> option = None
一方で、Noneではないリーフが含まれている場合は、Someでラップされた通常のツリーを返せます:
> Tree.node "Foo" [Leaf (Some 42); Leaf None; Leaf (Some 2112)] |> Tree.choose id;;
val it : Tree<string,int> option = Some (Node ("Foo",[Leaf 42; Leaf 2112]))
このとき、ツリー全体はSomeに包まれますが、リーフに含まれる値はラップされていません(Someの中身として通常の値が入っています)。
Bifunctor、Functor、そしてFold
Haskellは型クラスの機能を通じて、ファンクター(functor)、バイファンクター(bifunctor)、および他の種類のfold(リスト指向のカタモルフィズム)を形式的に定義できます。しかしF#にはそのような形式的な枠組みはありません。とはいえ、対応する機能を実装することは可能であり、関数名や使い方の慣習によって認識可能にできます。
まずはバイファンクター(bifunctor)としての機能から始めると簡単です:
// ('a -> 'b) -> ('c -> 'd) -> Tree<'a,'c> -> Tree<'b,'d>
let bimap f g = cata (f >> node) (g >> leaf)
これは、構文の違いを除けば、Haskellでの実装とほぼ同じです。このbimapを使えば、mapNodeやmapLeafといった関数も簡単に実装できますが、この記事のコードでは必要ありません。ただし、ここではmapLeafの別名とみなせる関数を使います:
// ('b -> 'c) -> Tree<'a,'b> -> Tree<'a,'c>
let map f = bimap id f
これでTreeはファンクターになります。
ツリーをよりコンパクトな値に集約したい場面もあるため、いくつかの特殊なfoldも用意しておきましょう:
// ('c -> 'a -> 'c) -> ('c -> 'b -> 'c) -> 'c -> Tree<'a,'b> -> 'c
let bifold f g z t =
let flip f x y = f y x
cata (fun x xs -> flip f x >> List.fold (>>) id xs) (flip g) t z
// ('a -> 'c -> 'c) -> ('b -> 'c -> 'c) -> Tree<'a,'b> -> 'c -> 'c
let bifoldBack f g t z = cata (fun x xs -> List.foldBack (<<) xs id >> f x) g t z
F#の命名規則に倣って、関数にはこのような名前を付けています。ListやOptionモジュールにも似たような関数があります。もし前回のHaskellの記事とF#のコードを比較している場合は、Tree.bifoldがbifoldlに、Tree.bifoldBackがbifoldrに相当します。
これらの関数を使えば、リーフだけに対するfoldも実装できます:
// ('c -> 'b -> 'c) -> 'c -> Tree<'a,'b> -> 'c
let fold f = bifold (fun x _ -> x) f
// ('b -> 'c -> 'c) -> Tree<'a,'b> -> 'c -> 'c
let foldBack f = bifoldBack (fun _ x -> x) f
これらの関数はさらに、この記事で役立つ別の関数の実装につながります:
// ('b -> unit) -> Tree<'a,'b> -> unit
let iter f = fold (fun () x -> f x) ()
画像アーキビストのプログラムでは、これらすべてを明示的に使うわけではありませんが、間接的には使用されます。
画像の移動
ここまでに紹介したコードは、いずれも画像ファイルに特化していないため、汎用的な再利用可能ライブラリに含めることができます。一方で、この記事の残りのコードはこのプログラム固有のものになります。ドメインモデルに関するコードは、Archiveという別モジュールにまとめることにします。記事の後半では、ファイルシステムからツリーを読み込む方法も紹介しますが、ひとまずここではそうしたツリーが既にあるものとして話を進めます。
このプログラムの主なロジックは、ソースツリーに基づいて、移動先となるディレクトリ構造のツリー(=目的ツリー)を作成することです。リーフノードにはファイルパス以外にも追加情報を持たせる必要があるため、それを表現する型を定義しましょう:
type PhotoFile = { File : FileInfo; TakenOn : DateTime }
PhotoFile型は、画像ファイルのパスに加えて、画像が撮影された日時を保持しています。この日時情報は、ファイルのメタデータから取得できますが、それは副作用を伴う処理なので、プログラムの冒頭で処理を委任することになります(この点については後ほど説明します)。
PhotoFileをリーフに持つソースツリーが得られれば、プログラムはそこからファイルの移動先を表すツリー(目的ツリー)を生成できます:
// string -> Tree<'a,PhotoFile> -> Tree<string,FileInfo>
let moveTo destination t =
let dirNameOf (dt : DateTime) = sprintf "%d-%02d" dt.Year dt.Month
let groupByDir pf m =
let key = dirNameOf pf.TakenOn
let dir = Map.tryFind key m |> Option.defaultValue []
Map.add key (pf.File :: dir) m
let addDir name files dirs =
Tree.node name (List.map Leaf files) :: dirs
let m = Tree.foldBack groupByDir t Map.empty
Map.foldBack addDir m [] |> Tree.node destination
このmoveTo関数は少し複雑に見えるかもしれませんが、実際には次の3つのステップで構成されています:
- 移動先フォルダを表すマップ(
m)を作成する。 - マップから枝(=サブディレクトリ)のリストを作成する(
Map.foldBack addDir m [])。 - 枝のリストを使ってツリーを構築する(
Tree.node destination)。
moveTo関数は、まず入力データを畳み込み処理してマップ(m)を作成します。このマップはディレクトリ名をキーとしていて、dirNameOf関数で生成されます。この関数はDateTime型の値を受け取り、YYYY-MM形式の文字列に変換します。たとえば、2018年12月20日は"2018-12"になります。
このマッピング処理によって、PhotoFileの値はMap<string, FileInfo list>型のマップにグルーピングされます。2014年4月に撮影された画像はキー"2014-04"に、2011年7月の画像はキー"2011-07"に、といった具合です。
次のステップでは、このマップをツリーの枝のリストに変換します。これらは移動先ディレクトリのサブディレクトリに相当します。目的のディレクトリ構造上は、各ノードがリーフのみを持つ浅い枝(shallow branches)となります。

残るステップは、この枝のリストをdestinationノードに追加するだけです。これは、パイプ演算子(|>)を使って枝のリストをTree.node destinationに渡すことで実現しています。
この関数は純粋関数なので、ユニットテストが非常に容易です。まずはテストケースを作って、関数を呼び出せばよいのです。
このコードベースでは、xUnit.net 2.4.1を使用しているので、テスト用のクラスとしてテストケースをまとめます:
type MoveToDestinationTestData () as this =
inherit TheoryData<Tree<string, PhotoFile>, string, Tree<string, string>> ()
let photoLeaf name (y, mth, d, h, m, s) =
Leaf { File = FileInfo name; TakenOn = DateTime (y, mth, d, h, m, s) }
do this.Add (
photoLeaf "1" (2018, 11, 9, 11, 47, 17),
"D",
Node ( "D", [Node ("2018-11", [Leaf "1"])]))
do this.Add (
Node ("S", [photoLeaf "4" (1972, 6, 6, 16, 15, 0)]),
"D",
Node ("D", [Node ("1972-06", [Leaf "4"])]))
do this.Add (
Node ("S", [
photoLeaf "L" (2002, 10, 12, 17, 16, 15);
photoLeaf "J" (2007, 4, 21, 17, 18, 19)]),
"D",
Node ("D", [
Node ("2002-10", [Leaf "L"]);
Node ("2007-04", [Leaf "J"])]))
do this.Add (
Node ("1", [
photoLeaf "a" (2010, 1, 12, 17, 16, 15);
photoLeaf "b" (2010, 3, 12, 17, 16, 15);
photoLeaf "c" (2010, 1, 21, 17, 18, 19)]),
"2",
Node ("2", [
Node ("2010-01", [Leaf "a"; Leaf "c"]);
Node ("2010-03", [Leaf "b"])]))
do this.Add (
Node ("foo", [
Node ("bar", [
photoLeaf "a" (2010, 1, 12, 17, 16, 15);
photoLeaf "b" (2010, 3, 12, 17, 16, 15);
photoLeaf "c" (2010, 1, 21, 17, 18, 19)]);
Node ("baz", [
photoLeaf "d" (2010, 3, 1, 2, 3, 4);
photoLeaf "e" (2011, 3, 4, 3, 2, 1)])]),
"qux",
Node ("qux", [
Node ("2010-01", [Leaf "a"; Leaf "c"]);
Node ("2010-03", [Leaf "b"; Leaf "d"]);
Node ("2011-03", [Leaf "e"])]))
かなりの行数に見えますが、実質的には単なるテストケースのリストです。各ケースは、ソースツリー・目的ディレクトリ名・期待される出力ツリーの三つ組です。
テスト本体のコードはコンパクトです:
[<Theory; ClassData(typeof<MoveToDestinationTestData>)>]
let ``Move to destination`` source destination expected =
let actual = Archive.moveTo destination source
expected =! Tree.map string actual
=!演算子はUnquoteから提供されているもので、「等しいはず」という意味です。もしexpectedとTree.map string actualが一致しなければ、例外が投げられます。
ここでactualをstringにマッピングしているのは、FileInfo型には構造的な等価性(Structural Equality)が定義されていないためです。FileInfoの等価性比較(およびTree<string, FileInfo>の比較)を自前で実装することもできますが、等価性のあるstringに変換した方が簡単なので、そうしています。
移動情報の計算
純粋な処理として、もうひとつ残っているステップがあります。それは、moveTo関数を呼び出して得られたツリーをもとに、実際にファイルを移動させるために、各ファイルについて「元のパス」と「移動先のパス」の両方を記録することです。この意図を明示するために、以下のような型を定義します:
type Move = { Source : FileInfo; Destination : FileInfo }
Moveは単なるデータ構造です。これは典型的なオブジェクト指向設計とは対照的です。オブジェクト指向では、こういった操作は(多くの場合ポリモーフィックな)メソッドとして実装されがちですが、関数型プログラミングでは、意図(intent) をデータとして表現することがよくあります。意図がデータである限り、それを柔軟に操作できますし、操作が完了した後は、インタプリタを使って目的の処理を実行できます。
前のmoveTo関数におけるユニットテストでは、ファイル名として "L" や "J"、"a" のような短いローカルファイル名を使っていました。これはテストを簡潔に保つためで、実際のところ、この関数は FileInfo オブジェクト自体の中身を直接扱ってはいません。
実際のユースケースでは、ファイル名はもっと長くなったり、ローカルパスではなくフルパス(例:"C:\foo\bar\a.jpg")が含まれていたりする可能性が高いでしょう。
moveToに、各リーフに完全なファイルパスが含まれるツリーを渡せば、出力ツリーは期待通りの構造を持つことになりますが、リーフには引き続き元ファイルのパスが入ったままです。したがって、各ファイルについてMove値を作成できます:
// Tree<string,FileInfo> -> Tree<string,Move>
let calculateMoves =
let replaceDirectory (f : FileInfo) d =
FileInfo (Path.Combine (d, f.Name))
let rec imp path = function
| Leaf x ->
Leaf { Source = x; Destination = replaceDirectory x path }
| Node (x, xs) ->
let newNPath = Path.Combine (path, x)
Tree.node newNPath (List.map (imp newNPath) xs)
imp ""
この関数は、Tree<string, FileInfo>を受け取り(moveToの出力と互換性があります)、Tree<string, Move>、すなわちリーフにMove値を持つツリーを返します。
先ほど「すべてのTree関連機能はcataで実装されている」と書きましたが、実は簡略化していました。calculateMovesの機能をcataで実装できるかというと、少なくとも私にはその方法がわかりません。しかし、パターンマッチと単純な再帰を使えば十分実装可能です。
このimp関数は、再帰的にツリーを辿りながらファイルパスを構築していきます。Leafノードが見つかったら、現在のFileInfoをSourceとし、たどってきたpathからDestinationを導き出して、Move値を作成します。
このコードもユニットテストしやすい構造になっています。まずはテストケースを定義します:
type CalculateMovesTestData () as this =
inherit TheoryData<Tree<string, FileInfo>, Tree<string, (string * string)>> ()
do this.Add (Leaf (FileInfo "1"), Leaf ("1", "1"))
do this.Add (
Node ("a", [Leaf (FileInfo "1")]),
Node ("a", [Leaf ("1", Path.Combine ("a", "1"))]))
do this.Add (
Node ("a", [Leaf (FileInfo "1"); Leaf (FileInfo "2")]),
Node ("a", [
Leaf ("1", Path.Combine ("a", "1"));
Leaf ("2", Path.Combine ("a", "2"))]))
do this.Add (
Node ("a", [
Node ("b", [
Leaf (FileInfo "1");
Leaf (FileInfo "2")]);
Node ("c", [
Leaf (FileInfo "3")])]),
Node ("a", [
Node (Path.Combine ("a", "b"), [
Leaf ("1", Path.Combine ("a", "b", "1"));
Leaf ("2", Path.Combine ("a", "b", "2"))]);
Node (Path.Combine ("a", "c"), [
Leaf ("3", Path.Combine ("a", "c", "3"))])]))
このパラメタライズドテストでは、各テストケースは入力ツリーと期待されるツリーのタプルです。テストでは、Archive.calculateMoves関数を使って変換を行い、出力ツリーが期待通りかを確認します:
[<Theory; ClassData(typeof<CalculateMovesTestData>)>]
let ``Calculate moves`` tree expected =
let actual = Archive.calculateMoves tree
expected =! Tree.map (fun m -> (m.Source.ToString (), m.Destination.ToString ())) actual
ここでも、比較のためにFileInfoをstringに変換しているのは、構造的等価性を保った比較を行うためです。
これで、目的とする機能を実現するための「純粋な」コード部分はすべて揃いました。あとは、ツリーをディスクから読み込む処理、そして結果ツリーをディスクに反映する処理(およびそれらを組み合わせる処理)を実装するだけです。
ディスクからのツリー読み込み
この記事の残りのコードはすべて不純(impure)な処理になります。これらを専用のモジュールに分けることもできますが、このプログラムで必要な不純な処理は、関数が3つと少しの構成コードだけなので、すべてProgramモジュールにまとめても問題ありません。私はそのようにしました。
ディスクからツリーを読み込むには、まずルートディレクトリが必要です。そのディレクトリの下にあるすべてのファイルとサブディレクトリを再帰的にたどって、木構造を作成します。次のような再帰関数を使って読み込みます:
// string -> Tree<string,string>
let rec readTree path =
if File.Exists path
then Leaf path
else
let dirsAndFiles = Directory.EnumerateFileSystemEntries path
let branches = Seq.map readTree dirsAndFiles |> Seq.toList
Node (path, branches)
この再帰関数は、まず指定されたpathが実在するファイルかどうかを確認します。もし存在すれば、それはファイルなので、そのパスを使って新たなLeafを作成します。
pathがファイルでない場合、それはディレクトリです。この場合は、Directory.EnumerateFileSystemEntriesを使って、そこに含まれるすべてのファイルとサブディレクトリを列挙し、それぞれを再帰的に処理します。これにより、現在のノードに対するすべての「枝」(branches)が得られます。最後に、それらの枝を使ってNodeを構築し、返します。
メタデータの読み込み
readTree関数は、リーフにstring(ファイルパス)を持つツリーを返します。しかし、プログラムが必要としているのは、リーフにPhotoFileを持つツリーです。そこで、各画像ファイルからExifメタデータを読み込み、ツリーを「撮影日時」情報で拡張する必要があります。
このコードベースでは、画像ファイルから必要なメタデータを抽出するために、Photoという小さなモジュールを用意しています。この記事ではそのすべてのコードは掲載しませんが、もしご興味があればGitHub上のコードをご覧ください。Photoモジュールを使うと、次のような不純な操作が実装できます:
// FileInfo -> PhotoFile option
let readPhoto file =
Photo.extractDateTaken file
|> Option.map (fun dateTaken -> { File = file; TakenOn = dateTaken })
この操作は、さまざまな理由で失敗する可能性があります:
- ファイルが存在しない
- ファイルにメタデータが存在しない
- メタデータはあるが、「撮影日時」が含まれていない
- 「撮影日時」が不正な文字列形式になっている
この関数readPhotoでTree<string, string>を走査すると、結果としてTree<string, PhotoFile option>が得られます。つまり、各ファイルについて「成功すればSome PhotoFile、失敗すればNone」という形になるのです。そして、ここで前述のTree.chooseが活躍します。その使い方は次のセクションで紹介します。
ツリーを書き出す
前述のcalculateMoves関数は、Tree<string, Move>を生成します。最後に必要な不純な処理は、このツリーをたどり、各Moveを実行することです:
// Tree<'a,Move> -> unit
let writeTree t =
let copy m =
Directory.CreateDirectory m.Destination.DirectoryName |> ignore
m.Source.CopyTo m.Destination.FullName |> ignore
printfn "Copied to %s" m.Destination.FullName
let compareFiles m =
let sourceStream = File.ReadAllBytes m.Source.FullName
let destinationStream = File.ReadAllBytes m.Destination.FullName
sourceStream = destinationStream
let move m =
copy m
if compareFiles m then m.Source.Delete ()
Tree.iter move t
writeTree関数は、入力として受け取ったツリーを走査し、各Moveに対して以下の処理を順に行います: 1. ファイルをコピーする 2. コピーが成功したかを検証する 3. 問題がなければ、元ファイルを削除する
合成
ここまでで紹介してきたすべての「レゴブロック(関数)」を組み合わせて、いわゆる不純/純粋/不純のサンドイッチを構築できます:
// string -> string -> unit
let movePhotos source destination =
let sourceTree = readTree source |> Tree.map FileInfo
let photoTree = Tree.choose readPhoto sourceTree
let destinationTree =
Option.map (Archive.moveTo destination >> Archive.calculateMoves) photoTree
Option.iter writeTree destinationTree
まず最初に、readTree関数を使ってsourceTreeを読み込みます。これによりTree<string, string>が得られるので、各リーフをFileInfoオブジェクトに変換します。次に、Tree.choose readPhotoで画像のメタデータを読み込みます。readPhotoはPhotoFile optionを返すので、Tree.chooseを使ってNoneを取り除きます。
この2行が、サンドイッチの「最初の不純なステップ」にあたります(比喩が混ざっているのは承知しています…)。
サンドイッチの「純粋な部分」は、純粋関数であるmoveToとcalculateMovesの合成です。ただし、photoTreeの型はTree<string, PhotoFile> optionなので、この合成はOption.mapの中で行う必要があります。結果として、destinationTreeはTree<string, Move> optionとなります。
最後の不純なステップは、writeTreeを使ってすべてのMoveを実行することです。
実行
movePhotos関数は、sourceとdestinationという引数を取ります。理論的には、これをリッチクライアントアプリやバックグラウンドプロセスから呼び出すこともできますが、この記事ではコマンドラインプログラムから呼び出すことにします。main関数では、引数を解析してmovePhotosを呼び出す必要があります:
[<EntryPoint>]
let main argv =
match argv with
| [|source; destination|] -> movePhotos source destination
| _ -> printfn "Please provide source and destination directories as arguments."
0 // return an integer exit code
引数の解析をより高度にすることもできますが、この記事の目的ではないため、プログラムを動かすのに最低限必要な処理だけを書いています。
これで、プログラムをコンパイルして実行できるようになりました:
$ ./ArchivePictures "C:\Users\mark\Desktop\Test" "C:\Users\mark\Desktop\Test-Out"
Copied to C:\Users\mark\Desktop\Test-Out\2003-04\2003-04-29 15.11.50.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2011-07\2011-07-10 13.09.36.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2014-04\2014-04-18 14.05.02.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2014-04\2014-04-17 17.11.40.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2014-05\2014-05-23 16.07.20.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2014-06\2014-06-21 16.48.40.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2014-06\2014-06-30 15.44.52.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2016-05\2016-05-01 09.25.23.jpg
Copied to C:\Users\mark\Desktop\Test-Out\2017-08\2017-08-22 19.53.28.jpg
実際にこのコマンドを実行すると、期待通りの移動先ディレクトリ構造が生成されます。
理論だけでなく、実際にも期待通りに動作すると嬉しいものですね。
まとめ
関数型ソフトウェアアーキテクチャでは、「純粋なコード」と「不純なコード」を分離し、純粋な関数が不純な操作を呼び出さないように設計します。多くの場合、私はこれを「不純/純粋/不純のサンドイッチ」アーキテクチャと呼んでいます。この記事では、ファイルシステムをツリーとしてモデリングする方法を紹介しました。これにより、不純なファイル操作と純粋なプログラムロジックとを分離することが可能になります。