アルゴリズム再入門
2012-07-16 14:25:12
![WEB+DB PRESS総集編[Vol.1~36]](https://gihyo.jp/assets/images/cover/2007/thumb/TH160_9784774130729.jpg)
WEB+DB Press 総集編[Vol.1〜36]に書いた記事『Webエンジニアのための基礎,徹底理解 3章:アルゴリズム再入門 C#編』を公開します。
ちなみにこの記事ではデータ構造についての話を最小限にしています。出てくるデータ構造は配列と二分木だけ。それは、データ構造については別のライターさんが記事を書くことになっていたからです。
ちなみに、書いてみたかった(というか、書いてみたけどやめた)アルゴリズムは、
- ハッシュ法 (これはデータ構造の章にあります。すばらしいです)
- 木の探索 (traversal)
- 平衡木 (AVLとか)
- その他の有名なソート (バブルソート、シェルソート、ヒープソート、etc)
- Skip List (これはどちらかと言うとデータ構造メインな話なのでためらった)
- BM法 (というかQuick Searchのほうが簡潔なのでそっち)
など。それから、数学的なアルゴリズム話(エラトステネスのふるいとか、ニュートン法とか、モンテカルロ法とか)も……
アルゴリズムとは?
「アルゴリズム」って何でしょうか。中学や高校の情報で勉強した人もいるかもしれませんが、簡単におさらいしておきます。
「アルゴリズム」を一言で言うと、仕事をやりとげるための作業手順を並べたものになります。本来は数学用語ですが、日常生活にもアルゴリズムを見つけることはできます。たとえば、インスタント焼きそばのアルゴリズムはこんな感じでしょう。
お湯を沸かす→ふたを開ける→かやく袋とソース袋を取り出す→かやくを乗せる→麺が浸るまでお湯を容器に注ぐ→ふたをかぶせる→3分程度待つ→ふたの湯切り口からお湯をすべて捨てる→ふたを開ける→ソースをかける→かきまぜる
一つ一つの手順だけを取り出してみても役には立ちませんが、それらが組み合わさることで、私達は味がまろやかな焼きそばを食べることができるのです。(この「組み合わさって意味がある」ところをフィーチャーしたのが「ピタゴラスイッチ」の「アルゴリズムたいそう」1なんでしょうね。)
ただし数学におけるアルゴリズムはもっと定義が細かくなっています。数学の場合は、「仕事の手順」じゃなくて「計算の手順」となります。そして、入力データとそれに対する答えがあること、特定のデータじゃなくても正しい答えが出ること、入力データが同じなら答えも同じになること、そして、手順にそって計算すればいつかは必ず答えが出ること、といった性質を持ったものをアルゴリズムといいます。
アルゴリズムとプログラムってどう違うの?一緒じゃないの?という疑問を持った人は鋭いです。実際、前にあげた「仕事をやりとげるための作業手順を並べたもの」という定義からみれば違いはありません。
ただしプログラムは、コンピュータの種類やOSやプログラミング言語に依存するものです。VBのプログラムをPerlとして実行することはできませんね。また、プログラムには変数定義だとかキーボートからの入力だとか画面出力だとかいったような、細かな処理もすべて書かないといけません。
一方アルゴリズムは、そういった具体的なプログラムから、重要な部分だけを抜き出したものと考えることができます。アルゴリズムはプログラム言語によらない処理の本質を指します。ですから、あるひとつのアルゴリズムに対して、何通りものプログラムを書くことができます。アルゴリズムの方がプログラムよりも抽象度が高いのです。
アルゴリズムの効率と計算量
アルゴリズムの良し悪しについて聞いたことはありますか?アルゴリズムは仕事をやりとげるための作業手順ですから、結果が出ないのであれば論外ですが、きちんと結果が得られるアルゴリズムであれば問題ないような気がします。ところがそうではないのです。
たとえば、友達とゲームをするときなど、ランダムに順番を決めたいときのアルゴリズムを考えましょう。アルゴリズム1はみんなでじゃんけん。アルゴリズム2はくじ引き。人数が少ない場合は、くじを作るよりはじゃんけんしたほうが早いでしょう。ところが人数が増えてくると、単純なじゃんけんでは勝敗がつかなくなってくるので、くじを作って引いたほうが効率がいいですよね。
つまり、同じ仕事をするためのアルゴリズムでも、効率を比べてみると大きく違うということがあるのです。人生は短く、金は少ない。良いアルゴリズムというのは、効率の良いアルゴリズムのことです。
アルゴリズムの効率を比べる指標として、計算量という概念があります。計算量には、時間計算量と空間計算量の2種類があります。これはどういうことかというと、前者は計算にどれだけ時間がかかるかを表します。後者は計算にどれだけメモリが必要かを表します。言っていることはすごく単純ですね。
で、多くの場合、コンピュータでの処理においては、空間計算量よりも時間計算量の方が重視されます(メモリやディスクは年々大容量化してますしね)。なので以降では、特に断りなしに「計算量」と言った場合は時間計算量のことをさすものとします。
さて、計算量なのですが、実際にコンピュータに処理をさせてかかった時間を計ることはしません。アルゴリズムというのはプログラムによらない手順なのですから。したがって、処理ステップの回数がトータルで何回になるかを使って計算量を表します。
もちろん、処理回数は入力となるデータの大きさに依存します(じゃんけんの例を思い出してください)。つまり、入力データの大きさを変数nで表したときの処理回数はnの関数になるということです。
とはいっても、処理回数を厳密に表そうとすると複雑な式になってしまって、使い勝手がよくありません。したがって計算量を表す時は、nが非常に大きいときの近似式にします。また、その際に定数倍は無視して考えます。そのような近似式を、計算量のオーダー(次数)と言います。「nが増えていくときの、処理回数の増加率」を表していると考えてください2。
計算量のオーダーを表す時には「ビッグO (オー) 記法」という記法を使います。たとえば、計算量がnの定数倍で近似できる時には、O(n) と書き、計算量がn2の定数倍で近似できる時には、O(n2) と書きます。以降、アルゴリズムの計算量はこのビッグO記法で書きます。
サーチ
線形探索法
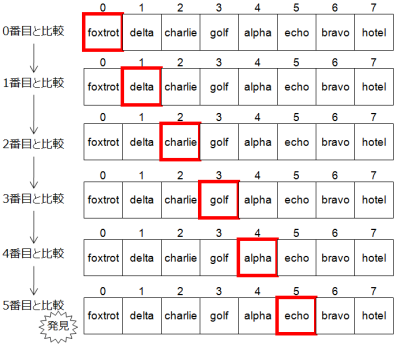
線形探索法(リスト1)は、データの最初から最後まで一つずつ順番に比較していき、求めるデータを探す方法です。下の例は、サイズ8 の文字列配列です。この中に“echo” という文字列が入っているかどうかを探してみましょう。
0番目は“foxtrot”、1番目は“delta”、……このように、先頭から順番に探していきます。そして、5番目で“echo”が見つかりました。
public int LinearSearch(string[] data, string value)
{
const int NOTFOUND = -1;
for (int i = 0; i < data.Length; i++)
{
// 値が見つかった場合は、その添字を返します。
if (data[i].Equals(value))
{
return i;
}
}
// 値が見つからなかったら-1を返します。
return NOTFOUND;
}
リスト1 線形探索法
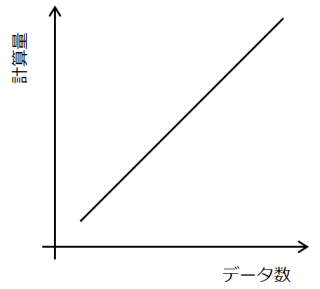
この方式だと、最悪の場合はデータ数の分だけ、平均でもデータ数の半分は比較を繰り返すことになります。よって計算量のオーダーはO(n)となります。
実際問題として、O(n)の計算量というのはそれほど悪いものではありません。しかし、データの並び方にある条件をつければ、より効率のいい探索ができます。
二分探索法
たとえば、データが小さい順、あるいは大きい順に並べられていたらどうでしょうか。実は、データが順番に並んでいた場合は、サーチに必要な計算量を大きく減らすことができるのです。では、実例で見てみましょう。
前の例ではデータは文字列だったので、辞書順に並べ替えてみます。この場合、二分探索法というアルゴリズムを適用できます。
二分探索法(リスト2)の考え方は、探索する範囲を半分ずつに狭めていき、最終的に探したいデータを見つける方法です。
やはり前と同じ例で見てみましょう。サイズ8の文字列配列ですが、今度はデータが辞書順に並んでいます。
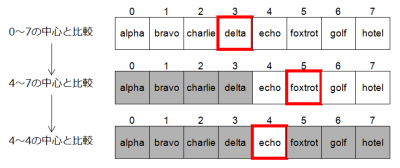
最初の探索位置として、 0番目から7番目までの中央を選びます。データは偶数個なので先頭に近いほうをとって、配列の3番目を見てみます。“delta”が入っていますので、“echo”はもっと後ろのほうに存在することが分かります。ということは、配列の0番目から3番目まではもう探索するまでもありません。よってそこは無視し、今度は配列の4番目から7番目の間で探せばよいことが分かります。
次の探索位置は、4番目から7番目までの中央なので、5番目ということになります。そこには“foxtrot”が入っていますので、“echo”はもっと前のほうに存在することが分かります。よって配列の5番目から7番目までは無視し、今度は配列の4番目から4番目までの間で探せばよいことが分かります。
そして、4番目から4番目までの中央なので、配列の4番目を調べます。もしここに“echo”が入っていなかったら、この配列にはそもそも“echo”という値が含まれていなかったことになります。さて実際には配列の4番目に“echo”が入っていましたから、探索終了です。
public int BinarySearch(string[] data, string value)
{
// dataはソート済みとします。
const int NOTFOUND = -1;
int start = 0;
int end = data.Length - 1;
while (start <= end)
{
int center = (start + end) / 2;
int compare = String.Compare(value, data[center]);
if (compare == 0)
{
// 値が見つかった場合は、その添字を返します。
return center;
}
if (compare < 0)
{
// 中央より前方を調べます。
end = center - 1;
}
else if (compare > 0)
{
// 中央より後方を調べます。
start = center + 1;
}
}
// 値が見つからなかったら-1を返します。
return NOTFOUND;
}
リスト2 二分探索法
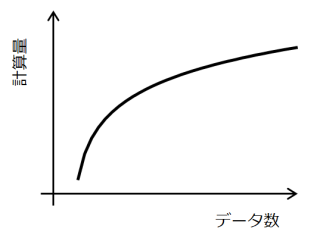
このような探索をすると、線形探索法よりもずっと効率よくデータを検索できます。計算量はどのようになるでしょうか。データの個数を2で割っていき、最終的に個数が1になるまで探索が繰り返されます(もちろん、運がよければもっと早くに見つかります)ので、繰り返しはlog2(n)回です。繰り返し1階につき比較を1回しますから、計算量のオーダーはO(log2(n))となります。
ソート
さて、前章でも出てきましたが、データのソートは基本的であり、よく使われます。多くのプログラミング言語では言語機能やライブラリとして提供されているほどです。とはいえ、ここではアルゴリズム再入門というテーマなのですから、ソートアルゴリズムもおさらいしながら、自分でコードを書けるぐらいになってしまいましょう。
選択ソート
最初のソートは選択ソートと呼ばれるアルゴリズムです。このアルゴリズムの発想は単純です。「未ソートのデータを全部調べて、一番[小さい または 大きい]ものを取り出して並べる」という手順を、未ソートのデータがなくなるまで繰り返すというものです。
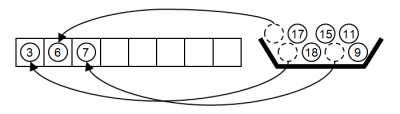
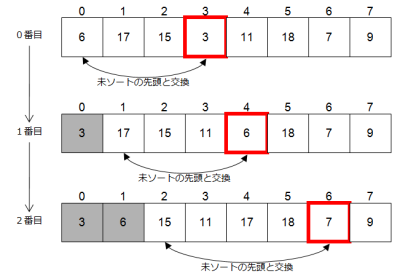
イメージとしては右図のようなものになるのですが、配列を使ってこの絵通りに実装しようとすると、未ソートの配列とソート済みの配列の2つを別々のメモリ上に持たないといけません。それは少々もったいないので(今時のコンピュータなら無視できる話なのですが)、1つの配列を使って同じことをやりましょう。つまり、1つの配列を未ソート部分とソート済み部分とで区別するのです。図にしてみました。未ソートの配列が順番にソート済みに置き換わっていく様子が分かると思います(リスト3)。
public void SelectionSort(int[] data)
{
for (int start = 0; start < data.Length - 1; start++)
{
// 未ソートのデータの先頭を最初の基準にします。
int smallest = start;
for (int i = start + 1; i < data.Length; i++)
{
if (data[i] < data[smallest])
{
// 最も小さいデータの位置を覚えておきます。
smallest = i;
}
}
// 最も小さいデータと先頭のデータを交換します。
int temp = data[start];
data[start] = data[smallest];
data[smallest] = temp;
}
}
リスト3 選択ソート
アルゴリズムは分かりやすいものだと思いますが、このアルゴリズムはデータ数が多いときに効率のよいものではありません。未ソート部分から一番[小さい または 大きい]ものを取り出すためには未ソート部を全部調べないといけませんし、それをデータ回数分だけ繰り返します。比較回数は n + (n-1) + … と足していって、+ 2 までの合計です。よって、計算量のオーダーはO(n2)となります。
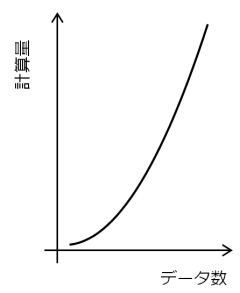
指数関数になるよりはマシですが、効率のよいアルゴリズムではありません。
マージソート
選択ソートは計算量がO(n2)となりました。ここから紹介するソートアルゴリズムは、計算量がO(n2)より小さくなるアルゴリズムです。代表例として、マージソートとクイックソートの2つを説明しましょう。
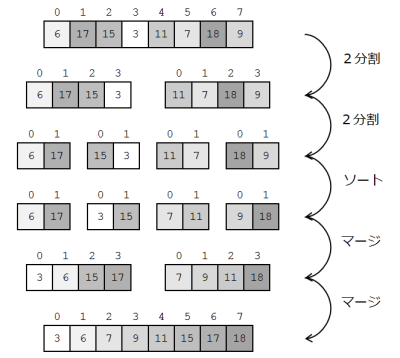
まずはマージソートです(リスト4)。マージソートでは、ソートしたい配列を2分割していき、すべての配列の要素数が2以下になったところでソートし、今度は繰り返しマージしていきます。
private int[] MergeSort(int[] data, int start, int end)
{
int count = end - start + 1;
// 個数が0以下の場合は空の配列を返します。
if (count < 1)
return new int[0];
// 個数が1の場合は要素数1の配列を返します。
if (count == 1)
return new int[1] { data[start] };
// 個数が2以上の場合は……
// まず、分割してソートします。
int center = (start + end) / 2;
int[] left = MergeSort(data, start, center);
int[] right = MergeSort(data, center + 1, end);
// そしてマージします。
int[] result = new int[count];
int l = 0;
int r = 0;
for (int i = 0; i < count; i++)
{
if ((l < left.Length) && (r < right.Length))
{
if (left[l] <= right[r])
{
// 左の配列から取り出します。
result[i] = left[l];
l++;
}
else
{
// 右の配列から取り出します。
result[i] = right[r];
r++;
}
}
else if (l >= left.Length)
{
// 左の配列は空なので、
// 右の配列から取り出します。
result[i] = right[r];
r++;
}
else
{
// 右の配列は空なので、
// 左の配列から取り出します。
result[i] = left[l];
l++;
}
}
return result;
}
リスト4 マージソート
このアルゴリズムの肝は、「ソート済み配列をマージして新たなソート済み配列を作る計算量は比較的小さい」というところにあります。
ではひとつ例を出してみます。大きさ4の配列AとBがあり、それぞれはすでに昇順にソートされています。それらをマージして、大きさ8の昇順ソート済み配列Cを作ってみましょう。
最初に、配列Cの0番目の値となる、最も小さい値を選び出します。配列Aの中の最小値は配列Aの0番目ですし、配列Bの中の最小値は配列Bの0番目です。よって最も小さい値というのは、その2つを比べたときの小さい方になります。ここでは配列Aの0番目である3が選ばれます。
続いて配列Cの1番目の値を選びます。配列Aの最小値は、0番目はすでに使われましたから1番目である6です。配列Bの最小値はやはり0番目である7です。6と7では6が小さいですから、配列Cの1番目は6です。
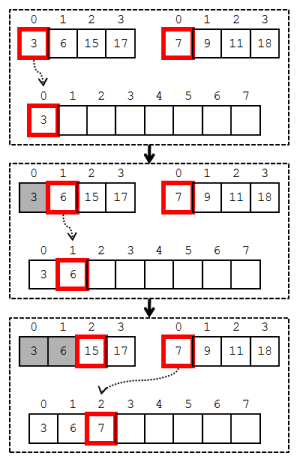
……とまあ、このようにマージは進んでいきます。値の小さいものを順に選び出していくということで選択ソートと似ていますが、その選び出していく時の手順が単純なのです。マージだけを考えれば、計算量はO(n)となっています。
もちろん、マージソートではマージを複数回繰り返しますから、トータルの計算量はn*(マージ回数)のオーダーとなります。そして、そのマージ回数なのですが、2分割を繰り返した分だけマージすることになりますから、回数はlog2(n)で表されます。結局、マージソートの計算量はO(n log2(n))となります。
え?計算量が本当に選択ソートより小さくなっているか、よくわからない?
前の方で、計算量 がO(n)の時とO(log2(n))の時のグラフを載せましたよね。あれを思い出してください。2つのグラフを比べると、nがとても大きくなると
となるのが分かると思います。
で、ここで両方をn倍しても結果は同じで、
となるわけです。
ところで、マージのためには、マージ前の配列とマージ後の配列の2つを別々のメモリ上に持たないといけません。しかも、選択ソートの時のような、1つの配列で済ませる良い方法はありません3。したがって、マージソートの場合、空間計算量はちょっと大きくなってしまいます。
クイックソート
続いてクイックソートです。クイックソートのアルゴリズムもソートしたい配列を分割していくアルゴリズムです(リスト5)。
まず、ソートしたい配列の中から適当なデータを選びます。選んだ値をピボットといいます。そしてピボットより小さいデータをピボットの前に、大きいデータを後ろに並べ替えます。
このようにすると、ピボットを中心として配列が二分割されます。その後、二分割されたデータに再び同じアルゴリズムを適用します。
そのようにして並べ替えと分割を繰り返すと最終的には長さが0または1になるので、そうなったらそこでピボットによる並べ替えと分割を止めます。
では実例を見てみましょう。今回は、分割対象の中心に位置するデータをピボットとして選ぶこととします。
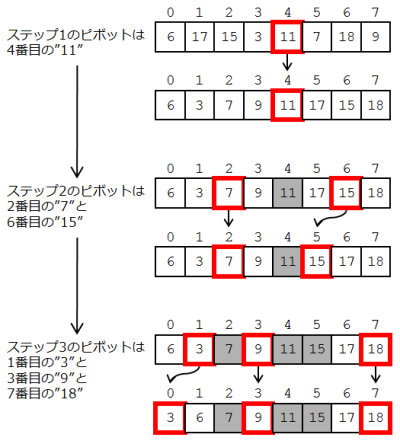
ステップ1では配列の0番目から7番目までを対象にします。ピボットとして、4番目の値である“11”を選んで並べ替えます。
ステップ2では配列の0から3番目、および5から7番目を対象にします。ピボットとして、2番目の値である“7”と、6番目の値である“15”を選んで並べ替えます。
ステップ3では配列の0から1番目、および6から7番目を対象にします。ピボットとして、1番目の値である“3”と、7番目の値である“18”を選んで並べ替えます。ここで分割結果の長さがすべて1以下になったのでアルゴリズムは終了です。
public void QuickSort(int[] data, int start, int end)
{
int count = end - start + 1;
if (count <= 1)
{
// 個数が1以下の場合はなにもしません。
return;
}
// ピボットを決定します。
int pivot = start + (count / 2);
int pivotValue = data[pivot];
// ピボットを基準に並べ替えます。
int s = start;
int b = end;
while (s < b)
{
while (data[s] < pivotValue)
{
// ピボット以上の値が見つかるまで後ろを調べます。
s++;
}
while (data[b] > pivotValue)
{
// ピボット以下の値が見つかるまで前を調べます。
b--;
}
// 交換します。
int temp = data[s];
data[s] = data[b];
data[b] = temp;
}
// sとbが一致した場所にピボットが移動しています。
QuickSort(data, start, s - 1);
QuickSort(data, b + 1, end);
}
リスト5 クイックソート
ではクイックソートの計算量を考えましょう。クイックソートの計算量は、(並べ替えの計算量)×(ステップ数)で表されます。
先にステップ数を考えましょう。ピボットとして選んだ値がデータの中心値であれば、1回の分割で長さが半分以下になりますから、ステップは最短で[log2(n)]回になります。しかし、ピボットがデータの最大値や最小値だった場合は、分割しても長さが1しか短くなりませんから、ステップは最長でn-1回になります。
次に並べ替えの計算量を考えます。実は、計算量がO(n)になるアルゴリズムがあります。言葉では説明しにくいので図を見てください。
並べ替え対象領域を配列a、領域の最初を指し示す変数をs、領域の最後を指し示す変数をbとします。
- sについて:
- a[s]がピボット以上であれば交換対象とする
そうでなければsを1つ後ろにずらす - bについて:
- a[b]がピボット以下であれば交換対象とする
そうでなければbを1つ前にずらす
このようにしてsとbをずらしていき、適宜a[s]とa[b]を交換していきます。すると、最後にはsとbが同じ位置を指し示しますから、そこで並べ替えは終了です。
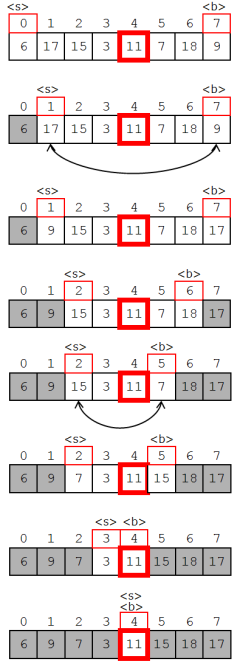
sとbをずらす回数はn-1回、その間にa[s]とa[b]を交換する回数は最大でもn-1回ですから、計算量はO(n)となるのです。
以上をまとめると、クイックソートの計算量は最良でO(n log2(n))になりますが、最悪の計算量はO(n2)になります。
二分木のアルゴリズム
ここでは、木構造、特に二分木に関するアルゴリズムを紹介します。木構造はデータ構造自体が再帰的のため、再帰を用いたアルゴリズムが適しています。
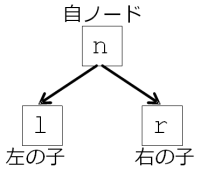
データ構造のページのおさらいになりますが、二分木とは、順序木(子ノードに順番がある木構造)のうち、子ノードが最大で2つまでしか存在しないようなものをいいます。そして二分木では、順序が先の子ノードを左の子、順序が後の子ノードを右の子と呼びます。
二分探索木
二分探索木とは、あるルールにしたがって構成された二分木です。そのルールとは、
あるノードの左の子孫にはすべて自ノードより小さい値が入り、右の子孫にはすべて自ノードより大きい値が入る
というものです(リスト6)。
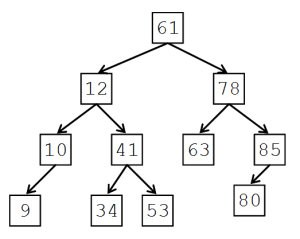
例を挙げてみましょう。下の図は正の整数を値にもつ二分探索木です。どのノードをとってみても、左の子孫には小さい値が、右の子孫には大きい値が入っていることが分かります。
このようなデータ構造を考えたときに問題となるのが、「値が同じものがあった場合はどうするのか?」ということです。それに対してはいくつかの解決法が考えられますが、本稿では二分探索木には同じ値を含まないものとします。
// 二分探索木のノード
public class Node
{
public int Value;
public Node Left;
public Node Right;
// コンストラクタ
public Node(int value)
{
this.Value = value;
}
}
// 二分探索木
public class BinarySearchTree
{
private Node root;
// 指定した値を持つノードを取得します。
public Node Search(int value)
{
// ルートを指定して二分探索木を探索。
return Search(root, value);
}
// 特定のノードを基点として
// 指定した値を持つノードを取得します。
private static Node Search(Node node, int value)
{
// 末端に達した場合はnullを返す。
if (node == null)
return null;
// キーがノードのキーよりも小さい場合は、
// 左の子を使用して再帰呼び出し。
if (value < node.Value)
return Search(node.Left, value);
// キーがノードのキーよりも大きい場合は、
// 右の子を使用して再帰呼び出し。
if (value > node.Value)
return Search(node.Right, value);
// どちらでもなければ、そのノードを返す。
return node;
}
// 指定した値を追加します。
public void Insert(int value)
{
// ルートが存在しない場合は、ルートを作成。
if (root == null)
root = new Node(value);
// そうでなければ、ルートを指定して値を追加。
else
Insert(root, value);
}
// 特定のノードを基点として
// 指定した値を追加します。
private static void Insert(Node node, int value)
{
// 追加する値がノードの値よりも小さい場合は……
if (value < node.Value)
{
// 左の子が存在しない場合は挿入
if (node.Left == null)
{
Node n = new Node(value);
node.Left = n;
}
// そうでなければ再帰呼び出し
else
{
Insert(node.Left, value);
}
}
// 追加する値がノードの値よりも大きい場合は……
if (value > node.Value)
{
// 右の子が存在しない場合は挿入
if (node.Right == null)
{
Node n = new Node(value);
n.Right = node.Right;
node.Right = n;
}
// そうでなければ再帰呼び出し
else
{
Insert(node.Right, value);
}
}
// 今回は、同じ値の場合は考慮しません。
}
}
リスト6 二分探索木
さて、この二分探索木から、特定の値を探索するアルゴリズムを考えてみましょう。例として、“34”という値を探してみます。
最初は根(ルート)を調べます。ここの値は61ですから、34が存在するなら左の子孫の中です。よって左の子に移動します。ここの値は12ですから、34が存在するなら右の子孫の中です。よって右の子に移動します。今度は値が41ですから、さらに左の子孫に移動します。すると値が34となり、めでたく探していた値が見つかりました。
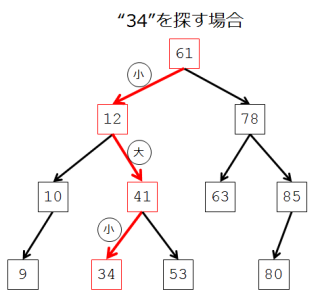
このように大小関係を比較しながら探索の範囲を狭めていく動作を見ると、二分探索法によく似ています。実際、もし二分探索木が左右でバランスのよい形をしていたならば、木の高さが[ log2(n) ]+1 となるので、計算量は 二分探索法と同じくO(log2(n))となります。
さらに二分探索木ならではのメリットは、データの挿入が高速なことです。二分探索法で使ったデータ構造は配列でした。配列の場合、途中にデータを挿入するためには、配列のサイズを拡張した上で、後続のデータを1つずつ後ろにずらさないといけません。これはO(n)の計算量となります。ところが二分探索木の場合は、子ノードを追加するだけであれば計算量はデータ量に関係ありませんから、O(1)となるのです。
とはいえ、二分探索木にも弱点があります。二分探索木の左右バランスが崩れた場合、たとえば下図のような形になった場合は、線形探索と同じく、探索の計算量はO(n)となってしまいます。
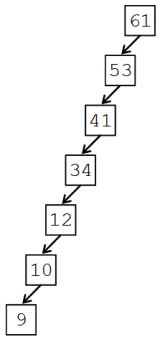
実際、データを大きい順(あるいは小さい順)に挿入すると、このようにバランスの崩れた二分探索木になってしまうのです。二分探索木を使うときは、木のバランスをどのように保つかが重要な問題となってきます4。
文字列の照合
長いテキストから特定の単語(パターン)を探し出したいという場合はよくあります。そのような問題を文字列の照合といいます。
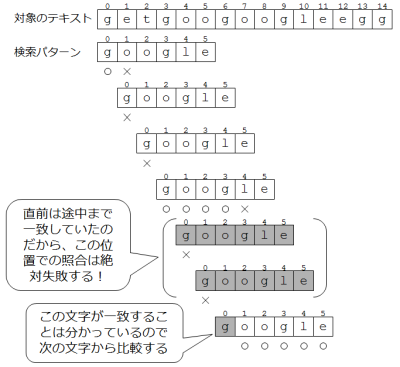
基本的には、テキストの先頭とパターンの先頭を揃えて、それから文字とパターンの文字を一文字ずつ比べていくことになります。比較の途中で文字が一致しない場合は、パターンの位置が悪かったということで、パターンの位置を後ろにずらして再度比較をやりなおします。そのようにしてパターンを後ろにずらしてゆき、パターンの最後まで文字が一致することがあった場合は、テキストに含まれるパターンを発見できたことになります。
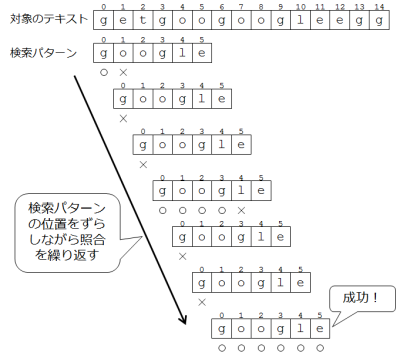
上の図はもっとも単純なアルゴリズムで、比較に失敗した場合はパターンを1つ後ろにずらすやり方です。このアルゴリズムだと最悪の場合の計算量が大きくなります。最悪の場合というのは、パターンの最後まで比較してはじめて比較失敗、というのをテキストの頭から終わりまで繰り返す場合です。対象テキストの長さをn、検索パターンの長さをmとすると、m回の比較をn回繰り返してしまいますから、計算量はO(mn)です。
KMP法
KMP法は、単純な文字列照合を改良して、最悪の場合でも計算量が大きくならないようにしたアルゴリズムです(リスト7)。
KMP法は、単純な照合アルゴリズムにあるムダを取り除く工夫をしています。具体的には、テキストに含まれる文字を何度も調べないようにします。
言葉だけだと分かりにくいので下の例を見てください。以下、対象テキストを文字列配列t, 検索パターンを文字列配列pとします。
t[0]から始めて、同じようにパターンをずらしていくのですが、t[3]から比較した場合がポイントです。その時、pとの照合は4文字まで成功し、5文字目で失敗します。
ここで、t[4] = p[1] = “o”であることが分かりましたので、パターンの位置を1つずらしても照合に失敗することは明らかです。同様に、t[5] = p[2] = “o”なので、パターンを2つずらしてもダメです。
その次、すなわちパターンを3つずらした場合はどうでしょうか。t[6] = p[3] = “g”なので、これはp[0]に一致しています。t[7]はp[4]と一致しないことしか分かっていませんから、t[7]とp[1]との比較から始めればいいことがわかります。
public int KnuthMorrisPratt(string s, string p)
{
const int NOTFOUND = -1;
if (String.IsNullOrEmpty(s))
return NOTFOUND;
if (String.IsNullOrEmpty(p))
return NOTFOUND;
// 補正値テーブルを作ります。
int[] c = GetCorrection(p);
int pos = 0; // パターンの位置
int i = 0; // テキストがパターンに一致した長さ
while ((pos + i < s.Length) && (i < p.Length))
{
if (s[pos + i] == p[i])
i++;
else
// パターンをずらします。
pos += (i - c[i]);
}
if (i == p.Length)
// パターンと一致する文字列が見つかりました。
return pos;
// 見つからなかったら-1を返します。
return NOTFOUND;
}
// 補正値テーブルを作成します。
private int[] GetCorrection(string p)
{
int[] result = new int[p.Length];
result[0] = -1;
int pos = 1; // パターンの位置
int i = 0; // パターンがパターン自身に一致した長さ
while ((pos + i < p.Length) && (i < p.Length))
{
if (p[pos + i] == p[i])
{
i++;
if (pos + i < p.Length)
result[pos + i] = i;
}
else
{
pos += (i - result[i]);
i = result[i];
if (i < 0)
i = 0;
}
}
return result;
}
リスト7 KMP法
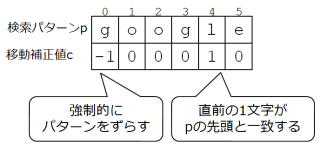
KMP法では、照合が途中で失敗した場合に検索パターンをどれだけずらせばいいかを、照合を始める前に計算しておきます。
原則として、p[i]の位置で照合が失敗した場合は、パターンの位置をiだけずらせば良いのですが、例外があります。まず、i=0、すなわち先頭で失敗した場合でもパターンを1ずらします。次に、p[i-1]以前の文字列が、pの先頭部分とc文字一致していた場合は、その位置に立ち返って照合しないといけないので、パターンはi-c しかずらす事ができません。
このように、パターンをずらすときの補正値cをテーブルにしたものが下図です。なお、下図の補正値cは「移動値をiからどれだけマイナスするか」を表したものになっています。
KMP法では、テーブルを作成する計算量はO(m)となります。また、実際の照合では、対象のテキスト1文字に対して、最大でも2回しか比較をしませんから、計算量はO(n)となります。両者を合わせて、計算量はO(m+n)となります。
おわりに
さて、有名どころのアルゴリズムを駆け足で振り返ってみましたが、いかがでしたか?
今回紹介できなかったアルゴリズムにも、有用なもの、高速なもの、興味深いもの、さまざまあります。本稿をきっかけにして、さらに深く学んでいただければ幸いです。
参考文献として2つ上げておきます。ひとつは『C言語による最新アルゴリズム事典』(技術評論社、ISBN: 978-4874084144)です。C言語が分かる人にはとっつきやすいでしょう。もうひとつは『Dictionary of Algorithms and Data Structures』( http://www.nist.gov/dads/ )です。アメリカ国立標準技術研究所のWebサイトで、英語なんですが、非常に多くのアルゴリズムとデータ構造が辞書の形にまとめられています。おすすめですよ。